Sisältö

• Askeleet

Trigonometrinen yhtälö sisältää muuttujan "x" (tai minkä tahansa muun muuttujan) yhden tai useamman trigonometrisen funktion. Trigonometrisen yhtälön ratkaiseminen on sellaisen arvon "x" löytäminen, joka täyttää toiminnot ja yhtälön kokonaisuudessaan.

• Trigonometristen yhtälöiden ratkaisut ilmaistaan ​​asteina tai radiaaneina. Esimerkkejä:

x = π / 3; x = 5π / 6; x = 3π / 2; x = 45 astetta; x = 37,12 astetta; x = 178,37 astetta.

• Huomaa: trigonometristen funktioiden arvot kulmista, ilmaistuna radiaaneina, ja kulmista, ilmaistuna asteina, ovat yhtä suuret. Trigonometristä ympyrää, jonka säde on yhtä kuin yhtä, käytetään trigonometristen funktioiden kuvaamiseen sekä trigonometristen perusyhtälöiden ja epätasa -arvojen ratkaisun oikeellisuuden tarkistamiseen.
• Esimerkkejä trigonometrisistä yhtälöistä:
  • sin x + sin 2x = 1/2; tg x + ctg x = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Trigonometrinen ympyrä, jonka säde on yksi (ympyräyksikkö).
   • Se on ympyrä, jonka säde on yhtä ja keskipiste pisteessä O. Yksikköympyrä kuvaa muuttujan "x" 4 trigonometristä perustoimintoa, missä "x" on kulma, joka mitataan X -akselin positiivisesta suunnasta vastapäivään.
   • Jos "x" on jokin kulma yksikköympyrässä, niin:
   • Vaaka -akseli OAx määrittää funktion F (x) = cos x.
   • Pystyakseli OBy määrittää funktion F (x) = sin x.
   • Pystyakseli AT määrittää funktion F (x) = tan x.
   • Vaaka -akseli BU määrittää funktion F (x) = ctg x.

• Yksikköympyrää käytetään myös ratkaisemaan trigonometriset perusyhtälöt ja eriarvoisuudet ("x": n eri sijainnit huomioidaan siinä).

Askeleet

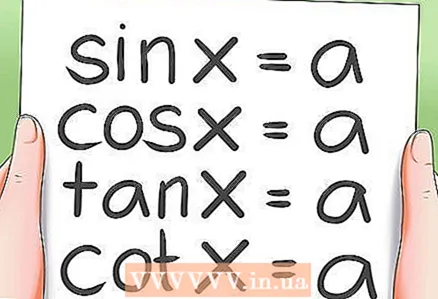1. 1 Käsite trigonometristen yhtälöiden ratkaisemiseksi.
   • Jos haluat ratkaista trigonometrisen yhtälön, muunna se yhdeksi tai useammaksi trigonometriseksi perusyhtälöksi. Trigonometrisen yhtälön ratkaiseminen johtaa lopulta neljän trigonometrisen perusyhtälön ratkaisemiseen.
2. 2 Trigonometristen perusyhtälöiden ratkaiseminen.
   • Trigonometrisia perusyhtälöitä on 4 tyyppiä:
   • sin x = a; cos x = a
   • tg x = a; ctg x = a
   • Trigonometristen perusyhtälöiden ratkaiseminen edellyttää yksikköympyrän eri x -sijaintien tarkastelua ja muuntotaulukon (tai laskimen) käyttöä.
   • Esimerkki 1.sin x = 0,866. Muuntotaulukon (tai laskimen) avulla saat vastauksen: x = π / 3. Yksikköympyrä antaa toisen vastauksen: 2π / 3. Muista: kaikki trigonometriset funktiot ovat jaksollisia, eli niiden arvot toistuvat. Esimerkiksi sinin x ja cos x jaksollisuus on 2πn ja tg x: n ja ctg x: n jaksollisuus on πn. Siksi vastaus kirjoitetaan seuraavasti:
   • x1 = π / 3 + 2πn; x2 = 2π / 3 + 2πn.
   • Esimerkki 2.cos x = -1/2. Muuntotaulukon (tai laskimen) avulla saat vastauksen: x = 2π / 3. Yksikköympyrä antaa toisen vastauksen: -2π / 3.
   • x1 = 2π / 3 + 2π; x2 = -2π / 3 + 2π.
   • Esimerkki 3.tg (x - π / 4) = 0.
   • Vastaus: x = π / 4 + πn.
   • Esimerkki 4. ctg 2x = 1,732.
   • Vastaus: x = π / 12 + πn.
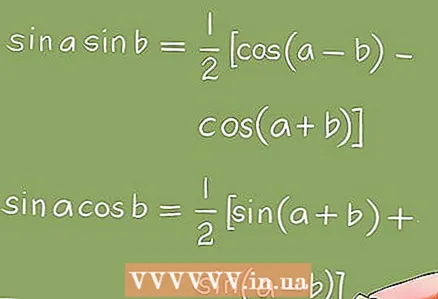3. 3 Muunnokset, joita käytetään trigonometristen yhtälöiden ratkaisemiseen.
   • Trigonometristen yhtälöiden muuntamiseen käytetään algebrallisia muunnoksia (factorization, homogeenisten termien vähentäminen jne.) Ja trigonometrisiä identiteettejä.
   • Esimerkki 5. Käyttämällä trigonometrisiä identiteettejä yhtälö sin x + sin 2x + sin 3x = 0 muunnetaan yhtälöksi 4cos x * sin (3x / 2) * cos (x / 2) = 0. Näin ollen sinun on ratkaise seuraavat trigonometriset perusyhtälöt: cos x = 0; sin (3x / 2) = 0; cos (x / 2) = 0.
     
     
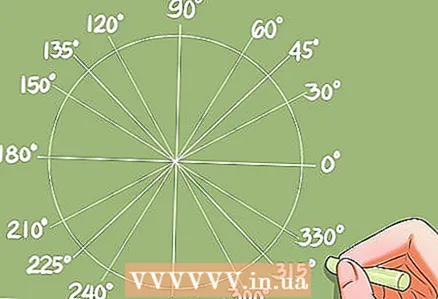
4. 4 Kulmien etsiminen funktioiden tunnetuista arvoista.
   • Ennen kuin opit menetelmiä trigonometristen yhtälöiden ratkaisemiseksi, sinun on opittava löytämään kulmat funktioiden tunnetuista arvoista. Tämä voidaan tehdä muuntotaulukon tai laskimen avulla.
   • Esimerkki: cos x = 0,732. Laskin antaa vastauksen x = 42,95 astetta. Yksikköympyrä antaa lisäkulmia, joiden kosini on myös 0,732.
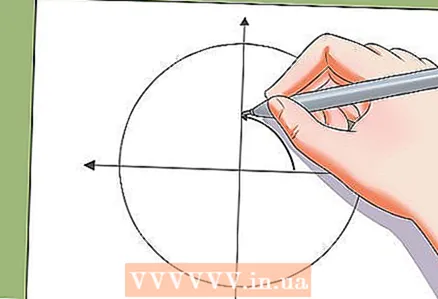5. 5 Aseta liuos sivuun yksikköympyrän päälle.
   • Voit lykätä ratkaisuja yksikköympyrän trigonometriselle yhtälölle. Yksikköympyrän trigonometrisen yhtälön ratkaisut ovat säännöllisen monikulmion kärkipisteet.
   • Esimerkki: Yksikköympyrän ratkaisut x = π / 3 + πn / 2 ovat neliön kärkiä.
   • Esimerkki: Yksikköympyrän ratkaisut x = π / 4 + πn / 3 edustavat säännöllisen kuusikulmion kärkiä.
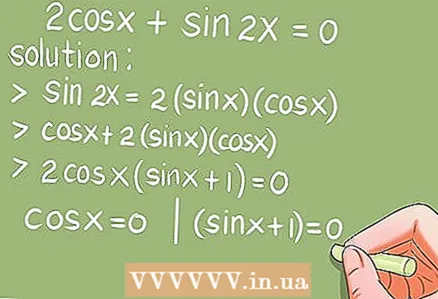6. 6 Menetelmät trigonometristen yhtälöiden ratkaisemiseksi.
   • Jos annettu trig -yhtälö sisältää vain yhden trig -funktion, ratkaise tämä yhtälö perus -trig -yhtälönä.Jos annettu yhtälö sisältää kaksi tai useampia trigonometrisiä funktioita, tällaisen yhtälön ratkaisemiseksi on kaksi tapaa (riippuen sen muuntumismahdollisuudesta).
     • Menetelmä 1.
   • Muunna tämä yhtälö muodoksi: f (x) * g (x) * h (x) = 0, jossa f (x), g (x), h (x) ovat trigonometriset perusyhtälöt.
     
     
   • Esimerkki 6.2cos x + sin 2x = 0. (0 x 2π)
   • Ratkaisu. Käytä kaksoiskulmakaavaa sin 2x = 2 * sin x * cos x, korvaa sin 2x.
   • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Ratkaise nyt kaksi trigonometristä perusyhtälöä: cos x = 0 ja (sin x + 1) = 0.
   • Esimerkki 7.cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • Ratkaisu: Muunna tämä yhtälö trigonometristen identiteettien avulla seuraavan yhtälön muotoon: cos 2x (2cos x + 1) = 0. Ratkaise nyt kaksi trigonometristä perusyhtälöä: cos 2x = 0 ja (2cos x + 1) = 0.
   • Esimerkki 8.sin x - sin 3x = cos 2x. (0 x 2π)
   • Ratkaisu: Muunna trigonometristen identiteettien avulla tämä yhtälö muodoksi: -cos 2x * (2sin x + 1) = 0. Ratkaise nyt kaksi trigonometristä perusyhtälöä: cos 2x = 0 ja (2sin x + 1) = 0.
     • Menetelmä 2.
   • Muunna annettu trigonometrinen yhtälö yhtälöksi, joka sisältää vain yhden trigonometrisen funktion. Korvaa sitten tämä trigonometrinen funktio tuntemattomalla, esimerkiksi t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t jne.).
   • Esimerkki 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π).
   • Ratkaisu. Korvaa tässä yhtälössä (cos ^ 2 x) (1 - sin ^ 2 x) (identiteetillä). Muunnettu yhtälö on:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Korvaa sin x t: llä. Yhtälö näyttää nyt tältä: 5t ^ 2 - 4t - 9 = 0. Tämä on toisen asteen yhtälö, jolla on kaksi juurta: t1 = -1 ja t2 = 9/5. Toinen juuri t2 ei täytä funktion arvoaluetta (-1 sin x 1). Päätä nyt: t = sin x = -1; x = 3π / 2.
   • Esimerkki 10. tg x + 2 tg ^ 2 x = ctg x + 2
   • Ratkaisu. Korvaa tg x t: llä. Kirjoita alkuperäinen yhtälö uudelleen seuraavasti: (2t + 1) (t ^ 2 - 1) = 0. Etsi nyt t ja etsi sitten x t = tg x: lle.
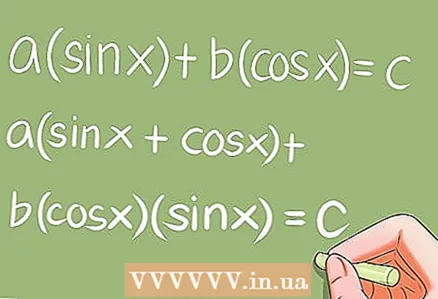7. 7 Erityiset trigonometriset yhtälöt.
   • On olemassa useita erityisiä trigonometrisiä yhtälöitä, jotka vaativat erityisiä muunnoksia. Esimerkkejä:
   • a * syn x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
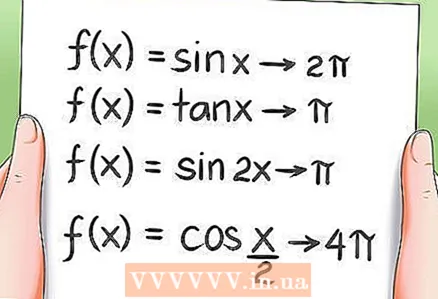8. 8 Trigonometristen funktioiden jaksollisuus.
   • Kuten aiemmin mainittiin, kaikki trigonometriset funktiot ovat jaksollisia, eli niiden arvot toistetaan tietyn ajan kuluttua. Esimerkkejä:
     • Funktion f (x) = sin x jakso on 2π.
     • Funktion f (x) = tan x jakso on yhtä suuri kuin π.
     • Funktion f (x) = sin 2x jakso on π.
     • Funktion f (x) = cos (x / 2) jakso on 4π.
   • Jos tehtävässä määritetään ajanjakso, laske arvo "x" tämän ajanjakson aikana.
   • Huomautus: Trigonometristen yhtälöiden ratkaiseminen ei ole helppo tehtävä ja johtaa usein virheisiin. Tarkista siis vastauksesi huolellisesti. Tätä varten voit piirtää graafisen laskimen avulla annetun yhtälön R (x) = 0. Tällaisissa tapauksissa ratkaisut esitetään desimaalimurtoina (eli π korvataan arvolla 3.14).