Sisältö

• Askeleet
• Menetelmä 1: 3: Osa 1: Kääntymispisteen määrittäminen
• Menetelmä 2/3: Funktion johdannaisten laskeminen
• Tapa 3/3: Osa 3: Etsi taivutuspiste
• Vinkkejä

Differentiaalisessa laskennassa taivutuspiste on käyrän piste, jossa sen kaarevuus muuttaa merkkiä (plus -miinuksesta tai miinuksesta plus -arvoon). Tätä konseptia käytetään konetekniikassa, taloudessa ja tilastoissa tunnistamaan merkittävät muutokset tiedoissa.

Askeleet

Menetelmä 1: 3: Osa 1: Kääntymispisteen määrittäminen

1. 1 Koveran funktion määritelmä. Koverin funktion kuvaajan minkä tahansa soinnun (segmentti, joka yhdistää kaksi pistettä) keskikohta sijaitsee joko kaavion alla tai sen päällä.
2. 2 Kupera funktion määritelmä. Kuperan funktion kuvaajan minkä tahansa soinnun (segmentti, joka yhdistää kaksi pistettä) keskikohta sijaitsee joko kaavion yläpuolella tai sen päällä.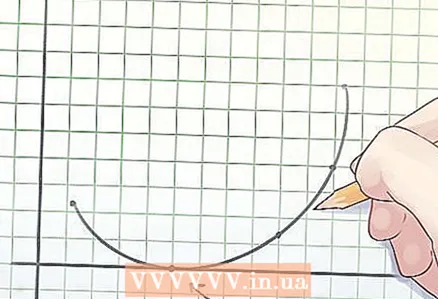
3. 3 Funktion juurien määrittäminen. Funktion juuri on muuttujan "x" arvo, jossa y = 0.
   • Kun piirretään funktiota, juuret ovat pisteitä, joissa kuvaaja ylittää x-akselin.

Menetelmä 2/3: Funktion johdannaisten laskeminen

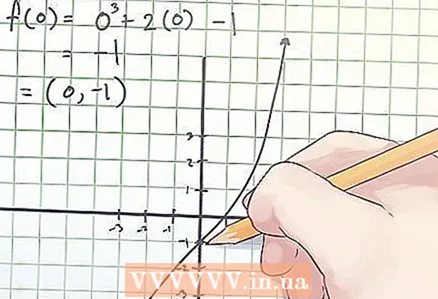
1. 1 Etsi funktion ensimmäinen derivaatta. Katso oppikirjan erilaistumissääntöjä; Sinun on opittava ottamaan ensimmäiset johdannaiset ja vasta sitten siirtymään monimutkaisempiin laskelmiin. Ensimmäiset johdannaiset on merkitty f '(x). Muodon ax ^ p + bx ^ (p - 1) + cx + d lausekkeiden ensimmäinen derivaatta on: apx ^ (p - 1) + b (p - 1) x ^ (p - 2) + c.
   • Etsi esimerkiksi funktion f (x) = x ^ 3 + 2x -1 taivutuspisteet. Tämän funktion ensimmäinen derivaatta on:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Etsi funktion toinen derivaatta. Toinen derivaatta on alkuperäisen funktion ensimmäisen derivaatan derivaatta. Toinen johdannainen on merkitty f ′ ′ (x).
   • Yllä olevassa esimerkissä toinen johdannainen on:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Aseta toinen derivaatta nollaksi ja ratkaise tuloksena oleva yhtälö. Tuloksena on odotettu taivutuspiste.
   • Yllä olevassa esimerkissä laskelmasi näyttää tältä:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Etsi funktion kolmas derivaatta. Varmistaaksesi, että tulos on todella käännepiste, etsi kolmas derivaatta, joka on alkuperäisen funktion toisen derivaatan derivaatta. Kolmas johdannainen on merkitty muodossa f ′ ′ (x).
   • Yllä olevassa esimerkissä kolmas johdannainen on:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Tapa 3/3: Osa 3: Etsi taivutuspiste

1. 1 Katso kolmas johdannainen. Taivutuspisteen arvioinnin vakiosääntö on, että jos kolmas derivaatta ei ole nolla (eli f ′ ′ (x) ≠ 0), taivutuspiste on todellinen taivutuspiste. Katso kolmas johdannainen; jos se ei ole nolla, olet löytänyt todellisen taivutuspisteen.
   • Yllä olevassa esimerkissä kolmas johdannainen on 6, ei 0.Joten olet löytänyt todellisen käännepisteen.
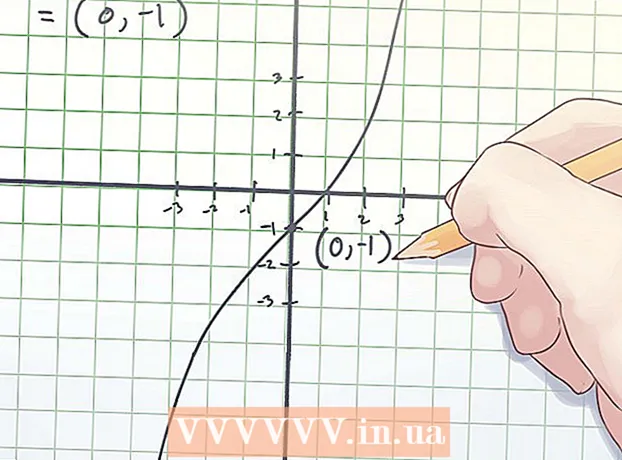
2. 2 Etsi taivutuspisteen koordinaatit. Taivutuspisteen koordinaatit on merkitty (x, f (x)), missä x on riippumattoman muuttujan "x" arvo taivutuspisteessä, f (x) on riippuvaisen muuttujan "y" arvo taivutuksessa kohta.
   • Yllä olevassa esimerkissä, kun yhtälität toisen derivaatan nollaksi, huomasit, että x = 0. Joten, määrittääksesi taivutuspisteen koordinaatit, etsi f (0). Laskentasi näyttää tältä:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
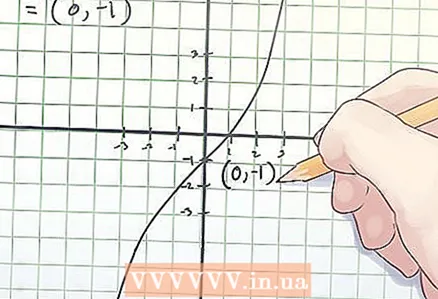3. 3 Kirjoita taivutuspisteen koordinaatit muistiin. Kääntöpisteen koordinaatit ovat löydetyt x- ja f (x) -arvot.
   • Yllä olevassa esimerkissä taivutuspiste on koordinaateissa (0, -1).

Vinkkejä

• Vapaan termin ensimmäinen derivaatta (alkuluku) on aina nolla.