Sisältö

• Askeleet

Etkö ole varma, miten työskennellä logaritmien kanssa? Älä huoli! Se ei ole niin vaikeaa. Logaritmi määritellään eksponentiksi, eli logaritminen yhtälöloki_ax = y vastaa eksponentiaalista yhtälöä a = x.

Askeleet

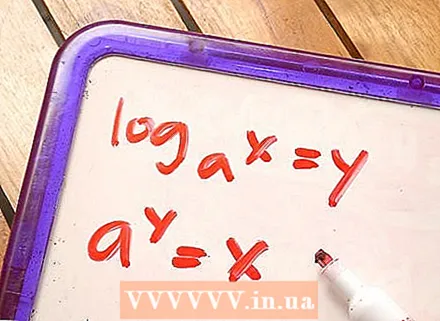1. 1 Ero logaritmisen ja eksponentiaalisen yhtälön välillä Jos yhtälö sisältää logaritmin, sitä kutsutaan logaritminen yhtälö (esim._ax = y). Logaritmi on merkitty logilla. Jos yhtälö sisältää asteen ja sen indikaattori on muuttuja, sitä kutsutaan eksponentiaaliseksi yhtälöksi.
   • Logaritminen yhtälö: log_ax = y
   • Eksponentiaalinen yhtälö: a = x
2. 2 Terminologia. Logaritmilokissa₂8 = 3 numero 2 on logaritmin perusta, numero 8 on logaritmin argumentti, numero 3 on logaritmin arvo.
3. 3 Ero desimaali- ja luonnollisten logaritmien välillä
   • Desimaalilogaritmit ovat logaritmeja, joiden pohja on 10 (esim. log₁₀x). Logaritmi, joka on kirjoitettu log x: ksi tai lg x: ksi, on desimaalilogaritmi.
   • Luonnolliset logaritmit ovat logaritmeja, joiden kanta on "e" (esimerkiksi log_ex). "E" on matemaattinen vakio (Eulerin luku), joka on yhtä suuri kuin raja (1 + 1 / n), kun n pyrkii äärettömyyteen. "E" on noin 2,72. Logaritmi, kirjoitettu muodossa ln x, on luonnollinen logaritmi.
   • Muut logaritmit... Kanta 2 logaritmeja kutsutaan binäärisiksi (esimerkiksi log₂x). Kanta 16 logaritmia kutsutaan heksadesimaaliksi (esimerkiksi loki₁₆x tai loki_{# 0f}x). Base 64 -logaritmit ovat niin monimutkaisia, että niihin sovelletaan mukautuvaa geometristä tarkkuuden säätöä (ACG).
4. 4 Logaritmien ominaisuudet. Logaritmien ominaisuuksia käytetään ratkaisemaan logaritmiset ja eksponentiaaliset yhtälöt. Ne ovat päteviä vain, kun sekä radix että argumentti ovat positiivisia lukuja. Lisäksi pohja ei voi olla 1 tai 0. Logaritmien ominaisuudet on annettu alla (esimerkkien kanssa).
   • Hirsi_a(xy) = loki_ax + loki_ay
     Kahden argumentin "x" ja "y" tuloksen logaritmi on yhtä suuri kuin "x": n ja "y": n logaritmin summa (vastaavasti logaritmien summa on yhtä suuri kuin niiden argumenttien tulo ).
     
     Esimerkki:
     Hirsi₂16 =
     Hirsi₂8*2 =
     Hirsi₂8 + loki₂2
   • Hirsi_a(x / y) = loki_ax - loki_ay
     Kahden argumentin "x" ja "y" osamäärän logaritmi on yhtä suuri kuin logaritmin "x" ja logaritmin "y" välinen ero.
     
     Esimerkki:
     Hirsi₂(5/3) =
     Hirsi₂5 - loki₂3
   • Hirsi_a(x) = r * loki_ax
     Argumentin "x" eksponentti "r" voidaan ottaa pois logaritmin merkistä.
     
     Esimerkki:
     Hirsi₂(6)
     5 * loki₂6
   • Hirsi_a(1 / x) = -log_ax
     Argumentti (1 / x) = x. Ja edellisen ominaisuuden mukaan (-1) voidaan ottaa pois logaritmin merkistä.
     
     Esimerkki:
     Hirsi₂(1/3) = -log₂3
   • Hirsi_aa = 1
     Jos argumentti on yhtä suuri kuin kanta, niin tällainen logaritmi on 1 (eli "a" 1: n tehoon on yhtä suuri kuin "a").
     
     Esimerkki:
     Hirsi₂2 = 1
   • Hirsi_a1 = 0
     Jos argumentti on 1, tämä logaritmi on aina 0 (eli "a" 0: n potenssiin on 1).
     
     Esimerkki:
     Hirsi₃1 =0
   • (Hirsi_bx / log_ba) = loki_ax
     Tätä kutsutaan logaritmin kannan muuttamiseksi. Kun jaetaan kaksi logaritmia samalla kannalla, saadaan yksi logaritmi, jossa perusta on yhtä suuri kuin jakajan argumentti ja argumentti on yhtä suuri kuin osingon argumentti. Tämä on helppo muistaa: alempi lokiargumentti laskee (tulee lopullisen logaritmin perustaksi) ja ylempi lokiargumentti nousee (tulee lopulliseksi lokiargumentiksi).
     
     Esimerkki:
     Hirsi₂5 = (log 5 / log 2)
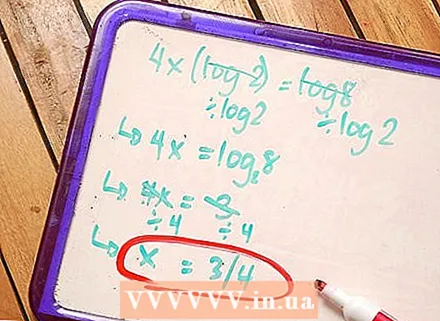5. 5 Harjoittele yhtälöiden ratkaisua.
   • 4x * log2 = log8 - Jaa yhtälön molemmat puolet log2: lla.
   • 4x = (log8 / log2) - käytä logaritmin kannan korvausta.
   • 4x = loki₂8 - Laske logaritmin arvo.
   • 4x = 3 - Jaa yhtälön molemmat puolet 4: llä.
   • x = 3/4 on lopullinen vastaus.