Kirjoittaja:
Clyde Lopez
Luomispäivä:
21 Heinäkuu 2021
Päivityspäivä:
1 Heinäkuu 2024
Sisältö
- Askeleet
- Menetelmä 1/2: Algebrallinen menetelmä
- Menetelmä 2/2: Graafinen menetelmä
- Vinkkejä
- Varoitus
Toiminnot voivat olla parillisia, parittomia tai yleisiä (eli ei parillisia tai parittomia). Toiminnon tyyppi riippuu symmetrian olemassaolosta tai puuttumisesta. Paras tapa määrittää funktion tyyppi on suorittaa sarja algebrallisia laskelmia. Mutta toiminnon tyyppi voidaan selvittää myös sen aikataulusta. Kun opit määrittelemään toimintojen tyypin, voit ennustaa tiettyjen toimintoyhdistelmien käyttäytymistä.
Askeleet
Menetelmä 1/2: Algebrallinen menetelmä
 1 Muista muuttujien vastakkaiset arvot. Algebrassa muuttujan vastakkainen arvo kirjoitetaan "-" (miinus) -merkillä. Lisäksi tämä pätee kaikkiin riippumattoman muuttujan nimityksiin (kirjaimella
1 Muista muuttujien vastakkaiset arvot. Algebrassa muuttujan vastakkainen arvo kirjoitetaan "-" (miinus) -merkillä. Lisäksi tämä pätee kaikkiin riippumattoman muuttujan nimityksiin (kirjaimella tai mikä tahansa muu kirje). Jos alkuperäisessä funktiossa muuttujan edessä on jo negatiivinen merkki, sen vastakkainen arvo on positiivinen muuttuja. Alla on esimerkkejä joistakin muuttujista ja niiden vastakkaisista merkityksistä:
- Päinvastainen merkitys
on
.
- Päinvastainen merkitys
on
.
- Päinvastainen merkitys
on
.
- Päinvastainen merkitys
 2 Korvaa selittävä muuttuja sen vastakkaisella arvolla. Eli käännä riippumattoman muuttujan merkki. Esimerkiksi:
2 Korvaa selittävä muuttuja sen vastakkaisella arvolla. Eli käännä riippumattoman muuttujan merkki. Esimerkiksi: muuttuu
muuttuu
muuttuu
.
 3 Yksinkertaista uusi toiminto. Tässä vaiheessa sinun ei tarvitse korvata tiettyjä numeerisia arvoja riippumattomalle muuttujalle. Sinun tarvitsee vain yksinkertaistaa uutta funktiota f (-x) verrataksesi sitä alkuperäiseen funktioon f (x). Muista eksponoinnin perussääntö: negatiivisen muuttujan nostaminen parilliseen potenssiin johtaa positiiviseen muuttujaan ja negatiivisen muuttujan nostaminen parittomaan potenssiin johtaa negatiiviseen muuttujaan.
3 Yksinkertaista uusi toiminto. Tässä vaiheessa sinun ei tarvitse korvata tiettyjä numeerisia arvoja riippumattomalle muuttujalle. Sinun tarvitsee vain yksinkertaistaa uutta funktiota f (-x) verrataksesi sitä alkuperäiseen funktioon f (x). Muista eksponoinnin perussääntö: negatiivisen muuttujan nostaminen parilliseen potenssiin johtaa positiiviseen muuttujaan ja negatiivisen muuttujan nostaminen parittomaan potenssiin johtaa negatiiviseen muuttujaan.  4 Vertaa kahta toimintoa. Vertaa yksinkertaistettua uutta funktiota f (-x) alkuperäiseen funktioon f (x). Kirjoita molempien toimintojen vastaavat termit toistensa alle ja vertaa niiden merkkejä.
4 Vertaa kahta toimintoa. Vertaa yksinkertaistettua uutta funktiota f (-x) alkuperäiseen funktioon f (x). Kirjoita molempien toimintojen vastaavat termit toistensa alle ja vertaa niiden merkkejä. - Jos molempien toimintojen vastaavien ehtojen merkit ovat samat, eli f (x) = f (-x), alkuperäinen funktio on parillinen. Esimerkki:
ja
.
- Tässä termien merkit osuvat yhteen, joten alkuperäinen toiminto on tasainen.
- Jos molempien funktioiden vastaavien ehtojen merkit ovat vastakkaisia, toisin sanoen f (x) = -f (-x), alkuperäinen funktio on parillinen. Esimerkki:
, mutta
.
- Huomaa, että jos kerrot jokaisen ensimmäisen funktion termin -1: llä, saat toisen funktion. Siten alkuperäinen funktio g (x) on pariton.
- Jos uusi funktio ei vastaa mitään yllä olevista esimerkeistä, se on yleinen funktio (eli ei parillinen eikä pariton). Esimerkiksi:
, mutta
... Molempien toimintojen ensimmäisten ehtojen merkit ovat samat, ja toisten ehtojen merkit ovat päinvastaisia. Siksi tämä toiminto ei ole parillinen eikä pariton.
- Jos molempien toimintojen vastaavien ehtojen merkit ovat samat, eli f (x) = f (-x), alkuperäinen funktio on parillinen. Esimerkki:
Menetelmä 2/2: Graafinen menetelmä
 1 Piirrä funktiokaavio. Käytä tätä varten piirtopaperia tai graafista laskinta. Valitse mikä tahansa numeroiden selittävien muuttujien arvojen monikerta
1 Piirrä funktiokaavio. Käytä tätä varten piirtopaperia tai graafista laskinta. Valitse mikä tahansa numeroiden selittävien muuttujien arvojen monikerta ja liitä ne funktioon riippuvaisen muuttujan arvojen laskemiseksi
... Piirrä pisteiden löydetyt koordinaatit koordinaattitasolle ja yhdistä nämä pisteet rakentaaksesi funktion kuvaajan.
- Korvaa funktion positiiviset numeeriset arvot
ja vastaavat negatiiviset numeeriset arvot. Esimerkiksi, kun otetaan huomioon toiminto
... Liitä seuraavat arvot
:
... Sain pisteen koordinaateilla
.
... Sain pisteen koordinaateilla
.
... Sain pisteen koordinaateilla
.
... Sain pisteen koordinaateilla
.
- Korvaa funktion positiiviset numeeriset arvot
 2 Tarkista, onko funktion kuvaaja symmetrinen y-akselin suhteen. Symmetria viittaa kaavion peilaukseen ordinaattiakselin ympäri. Jos kaavion osa y-akselin oikealla puolella (positiivinen selittävä muuttuja) on sama kuin y-akselin vasemmalla puolella oleva kuvaajan osa (selittävän muuttujan negatiiviset arvot), kuvaaja on symmetrinen noin Jos funktio on symmetrinen ordinaatin suhteen, funktio on parillinen.
2 Tarkista, onko funktion kuvaaja symmetrinen y-akselin suhteen. Symmetria viittaa kaavion peilaukseen ordinaattiakselin ympäri. Jos kaavion osa y-akselin oikealla puolella (positiivinen selittävä muuttuja) on sama kuin y-akselin vasemmalla puolella oleva kuvaajan osa (selittävän muuttujan negatiiviset arvot), kuvaaja on symmetrinen noin Jos funktio on symmetrinen ordinaatin suhteen, funktio on parillinen. - Voit tarkistaa kaavion symmetrian yksittäisten pisteiden perusteella. Jos arvo
joka vastaa arvoa
, vastaa arvoa
joka vastaa arvoa
, toiminto on tasainen.Esimerkissämme funktion kanssa
saimme seuraavat pisteiden koordinaatit:
- (1.3) ja (-1,3)
- (2.9) ja (-2,9)
- Huomaa, että kun x = 1 ja x = -1, riippuvainen muuttuja on y = 3 ja kun x = 2 ja x = -2, riippuvainen muuttuja on y = 9. Toiminto on siis tasainen. Itse asiassa funktion tarkan muodon selvittämiseksi sinun on otettava huomioon enemmän kuin kaksi kohtaa, mutta kuvattu menetelmä on hyvä likimäärä.
- Voit tarkistaa kaavion symmetrian yksittäisten pisteiden perusteella. Jos arvo
 3 Tarkista, onko funktion kuvaaja symmetrinen alkuperän suhteen. Alkuperä on piste, jolla on koordinaatit (0,0). Symmetria alkuperästä tarkoittaa, että positiivinen arvo
3 Tarkista, onko funktion kuvaaja symmetrinen alkuperän suhteen. Alkuperä on piste, jolla on koordinaatit (0,0). Symmetria alkuperästä tarkoittaa, että positiivinen arvo (positiivisella arvolla
) vastaa negatiivista arvoa
(negatiivisella arvolla
), ja päinvastoin. Parittomat funktiot ovat symmetrisiä alkuperän suhteen.
- Jos korvaamme funktiolla useita positiivisia ja vastaavia negatiivisia arvoja
, arvot
eroavat merkistä. Esimerkiksi, kun otetaan huomioon toiminto
... Korvaa siihen useita arvoja
:
... Sain pisteen koordinaateilla (1,2).
... Saimme pisteen koordinaateilla (-1, -2).
... Sain pisteen koordinaateilla (2,10).
... Saimme pisteen koordinaateilla (-2, -10).
- Siten f (x) = -f (-x), eli funktio on pariton.
- Jos korvaamme funktiolla useita positiivisia ja vastaavia negatiivisia arvoja
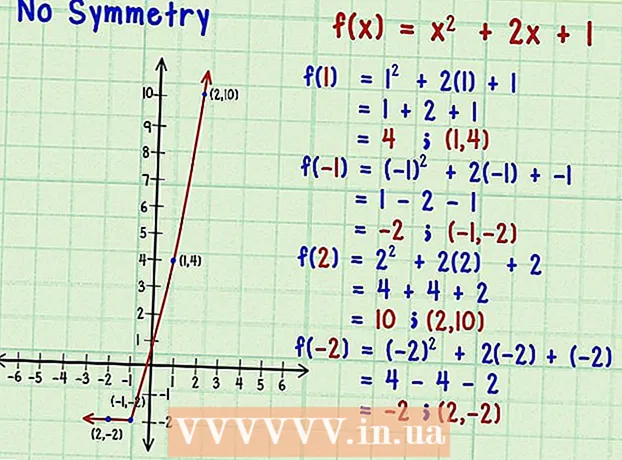
 4 Tarkista, onko funktion kaaviossa symmetriaa. Viimeinen funktiotyyppi on funktio, jonka kuvaajalla ei ole symmetriaa, eli peilausta ei ole sekä ordinaattiakselin että alkuperän suhteen. Esimerkiksi, kun otetaan huomioon toiminto
4 Tarkista, onko funktion kaaviossa symmetriaa. Viimeinen funktiotyyppi on funktio, jonka kuvaajalla ei ole symmetriaa, eli peilausta ei ole sekä ordinaattiakselin että alkuperän suhteen. Esimerkiksi, kun otetaan huomioon toiminto .
- Korvaa funktiolla useita positiivisia ja vastaavia negatiivisia arvoja
:
... Sain pisteen koordinaateilla (1,4).
... Saimme pisteen koordinaateilla (-1, -2).
... Sain pisteen koordinaateilla (2,10).
... Saimme pisteen koordinaateilla (2, -2).
- Saatujen tulosten mukaan symmetriaa ei ole. Arvot
päinvastaisille arvoille
eivät osu yhteen eivätkä ole päinvastaisia. Toiminto ei siis ole parillinen eikä pariton.
- Huomaa, että toiminto
voidaan kirjoittaa näin:
... Kun tämä muoto on kirjoitettu, funktio näyttää olevan jopa siksi, että parillinen eksponentti on läsnä. Mutta tämä esimerkki osoittaa, että funktion tyyppiä ei voida nopeasti määrittää, jos riippumaton muuttuja on suluissa. Tässä tapauksessa sinun on avattava hakasulkeet ja analysoitava vastaanotetut eksponentit.
- Korvaa funktiolla useita positiivisia ja vastaavia negatiivisia arvoja
Vinkkejä
- Jos riippumattoman muuttujan eksponentti on parillinen, funktio on parillinen; jos eksponentti on pariton, funktio on pariton.
Varoitus
- Tätä artikkelia voidaan soveltaa vain funktioihin, joissa on kaksi muuttujaa, joiden arvot voidaan piirtää koordinaattitasolle.



