Sisältö

• Askeleet
• Neuvoja

Jos olet matemaatikko tai graafinen ohjelmoija, sinun on todennäköisesti löydettävä kulma kahden annetun vektorin välillä. Tässä artikkelissa wikiHow näyttää, miten voit tehdä juuri sen.

Askeleet

Osa 1/2: Etsi kahden vektorin välinen kulma

1. 

   Vektorin määritelmä. Kirjoita kaikki tiedot kahdesta sinulla olevasta vektorista. Oletetaan, että sinulla on vain niiden koordinaattien määritetyt parametrit (kutsutaan myös komponenteiksi). Jos tiedät jo vektorin pituuden (suuruuden), voit ohittaa joitain alla olevia vaiheita.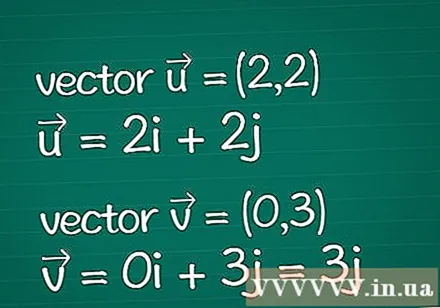
   • Esimerkki: Kaksiulotteinen vektori = (2,2) ja kaksiulotteinen vektori = (0,3). Ne voidaan kirjoittaa myös muodossa = 2i + 2j ja = 0i + 3j = 3j.
   • Vaikka tämän artikkelin esimerkissä käytetään kaksiulotteisia vektoreita, seuraavia ohjeita voidaan soveltaa mihin tahansa dimensioihin kuuluviin vektoreihin.

2. 

   
   
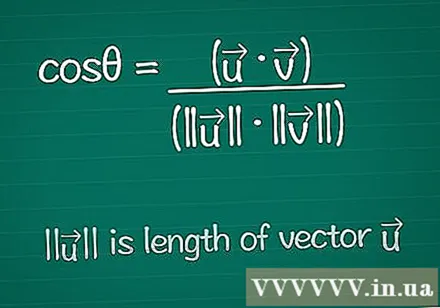
   Kirjoita kosinikaava. Kahden vektorin välisen kulman löytämiseksi aloitetaan kaavalla kosinin löytämiseksi tälle kulmalle. Voit oppia tästä kaavasta alla tai kirjoittaa sen vain näin:
   • cosθ = (•) / (|||| ||||)
   • |||| tarkoittaa "vektorin pituutta".
   • • on kahden vektorin skalaarinen tulo - tämä selitetään alla.

3. 

   
   
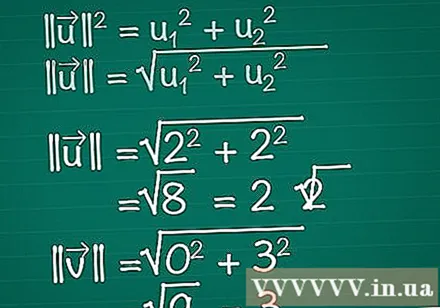
   Laske kunkin vektorin pituus. Kuvittele, että suorakulmio koostuu vektorin x: stä, y-komponenteista ja itse vektorista. Vektori muodostaa kolmion hypotenuusin, joten sen pituuden löytämiseksi käytämme Pythagorean teemaa. Itse asiassa tämä kaava voidaan helposti laajentaa mihin tahansa dimensioiden vektoriin.
   • || u || = u₁ + u₂. Jos vektorissa on enemmän kuin kaksi elementtiä, sinun on vain lisättävä + u₃ + u₄ +...
   • Näin ollen kaksiulotteiselle vektorille || u || = √ (u₁ + u₂).
   • Tässä esimerkissä |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
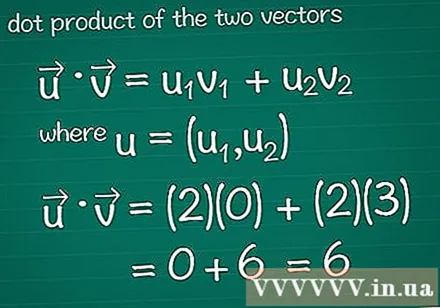
   Laske kahden vektorin skalaarinen tulo. Ehkä opit vektorikertoimen menetelmän, joka tunnetaan myös nimellä skalaari Tämä. Voit laskea skalaarisen tuotteen suhteessa niiden koostumukseen kertomalla ainesosat kumpaankin suuntaan yhdessä ja lisäämällä sitten koko tulos.
   • Katso grafiikkaohjelmaa kohdasta Vinkit ennen kuin luet lisää.
   • Matematiikassa • = u₁v₁ + u₂v₂, missä u = (u₁, u₂). Jos vektorissa on enemmän kuin kaksi elementtiä, lisää yksinkertaisesti + u₃v₃ + u₄v₄...
   • Tässä esimerkissä • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Tämä on vektorin ja vektorin skalaarinen tulo.

5. 

   Laita tulokset kaavaan. Muista, että cosθ = (•) / (|||| || ||). Nyt tiedämme sekä skalaarisen tuloksen että kunkin vektorin pituuden. Syötä nämä kaavaan kulman kosinin laskemiseksi.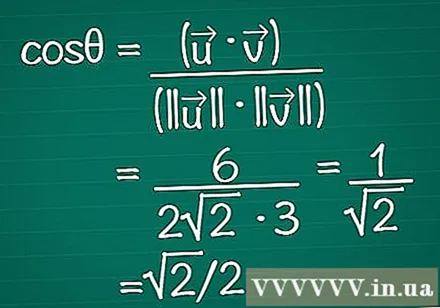
   • Esimerkissämme cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Etsi kulma sen kosinin perusteella. Voit käyttää arccos- tai cos-funktiota laskimessa löytääksesi θ tunnetusta cos-arvosta. Joidenkin tulosten avulla saatat löytää kulman yksikköympyrän perusteella.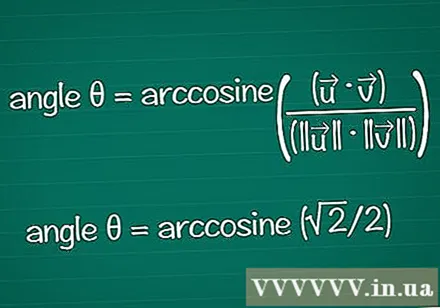
   • Esimerkissä cosθ = √2 / 2. Kirjoita kulmaan laskimessa "arccos (√2 ​​/ 2)". Tai löydät kulman θ yksikön ympyrästä, sijainnista cosθ = √2 / 2. Se pätee θ = /₄ tai 45 astetta.
   • Kaiken yhdistämällä lopullinen kaava on: kulma θ = arkosiini ((•) / (|||| || ||))
   mainos

Osa 2/2: Kulmakaavan määrittäminen

1. 

   Ymmärrä kaavan tarkoitus. Tätä kaavaa ei ole johdettu olemassa olevista säännöistä. Sen sijaan se muodostetaan skalaarisen tuloksen ja kahden vektorin välisen kulman määritelmänä. Silti se ei ollut mielivaltainen päätös. Palaten perusgeometriaan voimme ymmärtää, miksi tämä kaava tarjoaa intuitiiviset ja hyödylliset määritelmät.
   • Seuraavissa esimerkeissä käytetään kaksiulotteisia vektoreita, koska ne on helpoin ymmärtää ja yksinkertaisimpia. Kolmiulotteisilla tai useammilla vektoreilla on ominaisuudet, jotka määritellään melkein samanlaisilla yleisillä kaavoilla.

2. 

   Tarkasta Cosinen lause. Tarkastellaan tavallista kolmiota, jonka sivujen a ja b välinen kulma θ on vastakkaisella puolella c. Kosinilauseessa todetaan, että c = a + b -2abcos(θ). Tämä tulos saadaan yksinkertaisesti perusgeometriasta.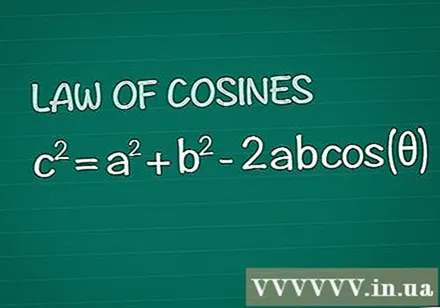

3. 

   Yhdistä kaksi vektoria muodostaen kolmion. Piirrä pari kaksiulotteista vektoria paperille, vektoreita ja vektoreita siten, että θ on niiden välinen kulma. Piirrä kolmas vektori näiden kahden välille muodostaaksesi kolmion. Toisin sanoen piirrä vektori siten, että + =. Vektori = -.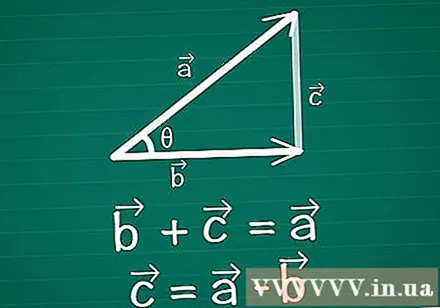

4. 

   Kirjoita tälle kolmiolle kosini-lause. Korvaa "vektorikolmion" sivupituus kosinilauseessa:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Kirjoita uudestaan ​​skalaarituotteella. Muista, että skalaarinen tulo on yhden vektorin kuva toisessa. Vektorin skalaarinen tulo itsessään ei vaadi projektiota, koska tässä ei ole eroa suunnassa. Tämä tarkoittaa • = || a ||. Tätä käyttämällä kirjoitamme yhtälön uudelleen:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Kirjoitti saman kaavan uudelleen. Laajenna kaavan vasenta puolta ja yksinkertaista sitten saadaksesi kaavan, jota käytetään kulmien löytämiseen.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   mainos

Neuvoja

• Jos haluat muuttaa arvoja ja ratkaista ongelman nopeasti, käytä tätä kaavaa mille tahansa kaksiulotteisen vektorin parille: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Jos työskentelet tietokonegrafiikkaohjelmiston kanssa, sinun on todennäköisesti huolehdittava vain vektorien ulottuvuudesta huolimatta niiden pituudesta. Lyhennä yhtälöä ja nopeuta ohjelmaa seuraavasti:
  • Normalisoi kukin vektori siten, että ne ovat yhtä suuret kuin 1. Voit tehdä tämän jakamalla vektorin komponentit sen pituudella.
  • Hanki skalaarin normalisoitu tulo alkuperäisen vektorin sijaan.
  • Koska pituus on 1, voimme jättää pituuselementit pois yhtälöstä. Lopuksi saatu kulmayhtälö on arccos (•).
• Kosinikaavan perusteella voimme nopeasti määrittää, onko kulma terävä vai tylsä. Aloita merkillä cosθ = (•) / (|||| ||||):
  • Yhtälön vasemmalla ja oikealla puolella on oltava sama merkki (positiivinen tai negatiivinen).
  • Koska pituus on aina positiivinen, cosθ: lla on oltava sama merkki kuin skalaarituotto.
  • Siksi, jos tuote on positiivinen, cosθ on myös positiivinen. Olemme yksikköympyrän ensimmäisessä kvadrantissa, with <π / 2 tai 90º. Löydettävä kulma on terävä kulma.
  • Jos skalaaritulos on negatiivinen, cosθ on negatiivinen. Olemme yksikköympyrän toisessa kvadrantissa, kun π / 2 <θ ≤ π tai 90º <θ ≤ 180º. Se on vankilanurkka.